Una equazione di primo grado è l’ UGUAGLIANZA di due espressioni algebriche che contengono una o più incognite (solitamente indicate con le lettere   “x”   “y”   “z”), UGUAGLIANZA verificata solo da UNO e UNO SOLO ben determinato valore da dare all’incognita. Per questo motivo, e anche per semplicità, da ora in poi la moltiplicazione (o prodotto) di due numeri o due lettere NON sarà più indicata con la classica croce (x) usata in aritmetica ma con un puntino tra i due numeri o addirittura nulla tra due lettere o tra un numero ed una lettera. Tutte le lettere dell’alfabeto (tranne la x, y e z) sono utilizzate al posto di numeri qualsiasi e NON rappresentano incognite da trovare. Quindi:

 

    3a          significa      3 moltiplicato per a

    4ax        significa      4 moltiplicato per a moltiplicato per x

 

A T T E N Z I O N E

1)      x + 2   =   x + 2

          NON E' UNA EQUAZIONE perchè rappresenta una UGUAGLIANZA SEMPRE VERA.

          Per questo motivo si chiama IDENTITA'.

2)       ci sono EQUAZIONI IMPOSSIBILI perchè NON hanno soluzioni. Ad esempio:

         x + 2   =   x + 3 

 

 

Tornando alle equazioni prendiamone una semplice:

 

            3x + 2 = 14

 

ed una complicata:

 

 

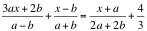
L’unica cosa che hanno in comune e che le caratterizza come equazioni è il segno “=” perché ripeto: l’equazione è l’uguaglianza di due espressioni algebriche.

 

Come in una bilancia a due bracci, tutto quello che sta a sinistra del segno “=” DEVE pesare quanto tutto ciò che sta a destra.

      

           

            2.2   COSA SIGNIFICA RISOLVERE UNA EQUAZIONE

 

Partiamo dalle equazioni di primo grado ad una incognita.

 

• Risolvere una equazione di primo grado significa cercare, trovare, calcolare (se esiste) QUEL ben determinato numero che sostituito all’incognita rende vera l’uguaglianza.

 

Partiamo da          3x + 2 = 14

 

Per quante prove possiate fare non troverete un altro numero (oltre “4”) che verifica questa uguaglianza, quindi  “4” è la soluzione, anzi:

la soluzione è:                       x = 4

 

E’ ovvio che non possiamo sperare di poter risolvere una qualsiasi equazione facendo chissà quante prove, anche perché la soluzione potrebbe essere una frazione o un numero decimale, pertanto ci serve un metodo, una strategia, un sistema per trovare QUEL valore della “x” che stiamo cercando.

Tornando alla nostra equazione possiamo vedere che

 

            partendo da:             3x + 2 = 14

            arriviamo a:              x = 4

 

Ciò significa che dobbiamo isolare la nostra “x” a destra del segno “=”, portando tutto il resto (in questo caso il 3 ed il 2) dall’altra parte.

 

            DOMANDA:   si può trasportare un termine da una parte all’altra del segno “uguale”?

                                   E se si, come si deve fare?

 

Non affrettatevi a rispondere “si, basta cambiare il segno” perché E’ SBAGLIATO!!!

Non solo è sbagliato, ma è la più grande bestialità del mondo aritmetico algebrico e matematico. E non importa se ve lo hanno insegnato a scuola! Dimenticate, anzi rimuovete dal cervello questa falsità perché vedrete che è la causa del 95% degli errori.

 

E’ fondamentale capire che ogni  numero nasce col suo segno (positivo o negativo) e non si può “cambiare il segno” di un numero.

Se verso in banca                 € 100,00       questo per me rappresenta un numero POSITIVO

Se prelevo dalla banca         €  200,00      questo per me rappresenta un numero NEGATIVO

 

Infatti, prima dell’avvento dei computers, gli impiegati di banca scrivevano le cifre dei versamenti con inchiostro NERO e i prelievi con inchiostro ROSSO, proprio per evitare che per sbaglio (o per truffa) il mio prelievo di 200,00€ potesse diventare un versamento solo correggendo il “-“ facendolo diventare “+”.

        

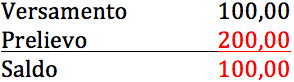
Da qui nasce il modo di dire “avere il conto corrente in rosso” o “andare in rosso” in banca.

 

Pertanto ogni numero dovrebbe essere scritto in nero o in rosso oppure col suo segno (che è immutabile) e dovremmo fare molta attenzione a distinguere il “segno” dalle “operazioni”.

 

Ad esempio:

al posto di:       3 + a – 4 + 8 – 5b         dovrei scrivere:            (+3) + (+a) – (+4) + (+8) + (-5b)

al posto di:       7a - 9b                         dovrei scrivere:            (+7)(+a) – (+9)(b)

 

Come vedete sarebbe tutto molto più lungo e complicato per cui scegliamo di usare il primo modo di scrittura, anche se così facendo rischiamo di confondere i “segni” con le “operazioni”.

Diciamo che in matematica si parla sempre e soltanto di “SOMME ALGEBRICHE”, cioè:

 

 

anche se poi nella pratica il “trattino” tra 34 e 21 lo consideriamo come “sottrazione”.

 

            2.3   COME SI RISOLVE UNA EQUAZIONE

 

Riprendiamo la nostra equazione                       3x + 2 = 14

che con vari passaggi deve diventare                  x = 4

 

Dobbiamo quindi portare sia il 3 che il 4

dall’altra parte dell’uguale, cioè                   x = 4  ;  3  ;  2            (non sappiamo ancora come “cucinare” questi numeri!)

 

1^a DOMANDA:       portiamo di là prima il (3) o prima il (2), ma

                               soprattutto come scegliere quale spostare per primo?

 

Immaginiamo che la nostra equazione non sia formata da numeri e lettere ma da oggetti concreti e proviamo a rappresentarla così:

         3  _*   x  +  2     =    14

                         

 

alla nostra “x” ci sono attaccati il “3”  ed il “2” con due legami (operazioni) diverse:

tra x e 3 c’è l’operazione  “≅” (prodotto) e tra x e 2 c’è l’operazione  “≈” (somma).

Abbiamo detto che il legame dell’operazione “prodotto” è più forte del legame dell’operazione “somma” (capitolo 1.3) per cui se prendiamo in mano l’oggetto             e tiriamo con forza per le due estremità è logico anzi ovvio che si romperà dove è più debole, cioè in una mano ci resterà     e nell’altra avremo   .

 

Un altro esempio ci può aiutare: se scuoto un albero di pere, quale frutto cascherà per primo? Certamente il più maturo, perché è quello “attaccato” al ramo più debolmente dei frutti acerbi.

 

Quindi: PRIMA si portano di là i termini sommati o sottratti POI quelli moltiplicati (o divisi)!

 

1.     3x + 2        = 4

2.     3x              = 4 , (((2)))

3.     x                = 4 , (((2))) , (((3)))

 

Analogamente la potenza è più forte della moltiplicazione e molto più forte della somma per cui:

 

1.     3x² + 5       = 53

2.     3x²                = 53 , (((5)))

3.     x²                = 53 , (((5))) , (((3)))

4.     x                 = 53 , (((5))) , (((3))) , (((2)))

 

Ecco dunque la

2.3-1^a  REGOLA:    per portare un termine da una parte all’altra dell’uguale

bisogna rispettare le precedenze:

• PRIMA i termini sommati o sottratti,
• POI quelli moltiplicati o divisi
• per ULTIME le potenze o le radici.

 

 

 

 

           2.4   SECONDA REGOLA FONDAMENTALE

 

Riprendiamo la nostra equazione             3x + 2 = 14

Abbiamo stabilito che il primo termine da spostare è il “2”. Possiamo limitarci a “prelevarlo” da sinistra e “trasferirlo” a destra?

Ovviamente no perché se consideriamo l’equazione come una bilancia che deve sempre rimanere in equilibrio, togliendo un oggetto da un piatto la bilancia si alza e se lo stesso oggetto lo poso sull’altro piatto l’effetto raddoppia!

 

Vediamolo con un esempio fatto con oggetti:

      

 

e con un esempio in cui gli "oggetti" sono i monomi dell' equazione: 

 

 

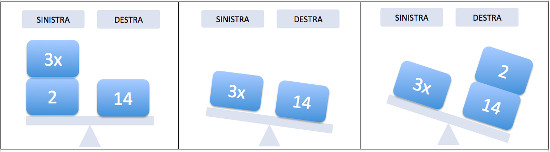
Quindi non possiamo limitarci semplicemente a “spostare” gli oggetti a nostro piacimento.

Ci serve una strategia efficace.

Se invece aggiungo ad entrambi i piatti della bilancia due oggetti uguali (uno in ciascun piatto) la bilancia rimane in equilibrio, vero?

La domanda è cosa aggiungere?

Abbiamo detto che somma e divisione sono operazioni una l’inverso dell’altra e che possiamo sempre trovare una sottrazione che elimina l’effetto di una somma e viceversa.

Allora, per eliminare il “+2” nel piatto di sinistra devo aggiungere un “-2” a sinistra ma contemporaneamente devo mettere un “-2” anche a destra per mantenere l’equilibrio.

Vediamo tutti i passaggi:

 

        

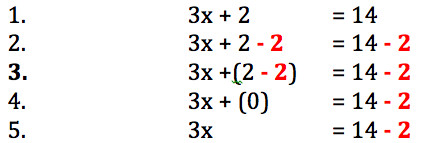
Se guardiamo solo il primo passaggio e l’ultimo

 

  

 

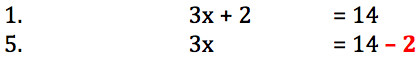
abbiamo tolto il “2” a sinistra ed è comparso un “2” a destra MA NON E’ LO STESSO “2”!

Quello a destra è uno dei due “oggetti” che ho aggiunto ad entrambi i piatti della bilancia (sono rossi per evidenziare meglio ciò che ho fatto).

A sinistra “+ 2” e “- 2” si sono annullati, a destra “- 2” è rimasto

Facciamo la semplificazione a destra e troviamo

 

                       3x = 14 – 2

                       3x = 12

 

Ora occupiamoci del numero “3”.

 

Rispetto alla “x” il “3” è moltiplicato, quindi se vogliamo eliminarlo dobbiamo DIVIDERE per “3” , ma non potendo farlo solo a sinistra, dividiamo per “3” entrambi i termini dell’equazione:

 

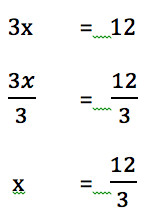
quindi semplifichiamo a destra e troviamo la nostra soluzione:

 

   x  =  4

 

Anche in questo caso il numero “3” che troviamo a destra NON E’ lo stesso “3” che era a sinistra ma uno dei due numeri che ho usato per dividere tutti e due i termini dell’equazione per eliminare il coefficiente della “x”.

 

Per ultimo consideriamo il caso in cui l’incognita sia elevata a potenza:

 

                         x²   =   9

 

Siccome l’inverso della potenza è la radice, mettiamo sotto segno di radice entrambi i termini:

 

 

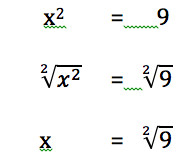
Come possiamo sintetizzare tutte queste procedure, o meglio cosa hanno in comune tutti questi passaggi? C’è una regola generale che valga sempre?

Riflettiamo: ciò che a sinistra era SOMMATO a destra diventa SOTTRATTO, ciò che era MOLTIPLICATO a sinistra diventa DIVISO, la POTENZA diventa RADICE (e viceversa).

Quindi:

 

 

2.4-2^a  REGOLA   si può spostare un termine da una parte all’altra dell’uguale a patto di:

 

1. RISPETTARE LE PRECEDENZE (prima i termini sommati o sottratti, poi quelli moltiplicati o divisi, per ultimi gli esponenti delle potenze e le radici)
2. INVERTIRE L’OPERAZIONE (ciò che è sommato diventa sottratto, ciò che è moltiplicato diventa diviso e la potenza diventa radice e viceversa)

 

Tutto questo viene egregiamente rappresentato da quella che io chiamo

 

dove in linea verticale dall’alto verso il basso vediamo le precedenze da rispettare ed in linea orizzontale vediamo come trasformare le operazioni quando dobbiamo spostare un termine di una equazione da una parte all’altra dell’uguale.

 

Quindi questa DOPPIA CROCE ci dice che

1. per calcolare una espressione aritmetica o algebrica bisogna partire dall'alto verso il basso, dalle operazioni più forti a quelle più deboli, perchè dobbiamo "compattare" tanti numeri fino ad averne uno solo (la soluzione dell'espressione) e siccome le operazioni legano due numeri alla volta, è chiaro che il legame più forte "opera" per primo e poi via via tutti gli altri.

2. per risolvere una equazione dobbiamo fare il percorso inverso, cioè liberare l'incognita da tutto ciò che ha "attaccato" intorno (a destra, a sinistra e in alto), come spacchettarla da tutti gli involucri che la contengono, quindi dobbiamo partire dal basso verso l'alto, da tutto ciò che è "attaccato" col legame più debole e poi salire di grado, ricordandoci di INVERTIRE l'operazione ogni volta che "spostiamo" un "oggetto".

    
    

ESERCIZI

 

ESERCIZIO 2.R-a

Trovare il valore della x:

1. 4x + 3  =  11                        5 punti
2. 2x - 5  =  x - 2                     5 punti
3. 5 - 2x  =  9 -6x                    5 punti
4. 2(x - 3)   =   2x - 6               7 punti
5. a(2x +3)  =  ax - a                8 punti

 

 

 

 

 

(1) Le operazioni     < (2) >     (3) Monomi e polinomi